【算法】 点分治总结&学习笔记 | Qiuly's blog!

【算法】 点分治总结&学习笔记

Posted on | Edited on | In | Comments:

其实很短的啦，感觉……感觉淀粉质这种东西好像没什么可以总结的……
只会有一些简单的板子题而已……(实际上是砍不动难的题目)
(淀粉质吗？味道真是不错呢嘿嘿嘿)

0XFF—-点分治是啥？

点分治，是处理树上路径的一个极好的工具。
一般如果需要大规模处理树上路径，点分治是一个不错的选择。
———一位网上的Dalao

现在有一个问题，给你一颗树，树上的每一条边都有权值，现在给一个 $k$ ，要求你求出树上所有路径中路径权值小于 $k$ 的路径总数，你怎么办？

暴力？$O(N^3)$ 的复杂度分分钟让你 T 飞！

当然，你可以用分治来求，复杂度仅有 $O(nlogn)$。

对于树上做分治，不仅有基于点的分治方式，还有基于边的以及基于链的，但是这不在我们的讨论范围类(作者太蒟了不会QvQ)。

0X1F 点分治的流程

0X1F—-1 怎么分治？

对于所有的路径，很显然我们可以将它们分成两部分：

  • $1.$ 这条路径经过了它所在的子树的根节点
  • $2.$ 这条路径没经过它所在的子树的根节点

假设现在有一颗树，Ta的根节点是 $1$：

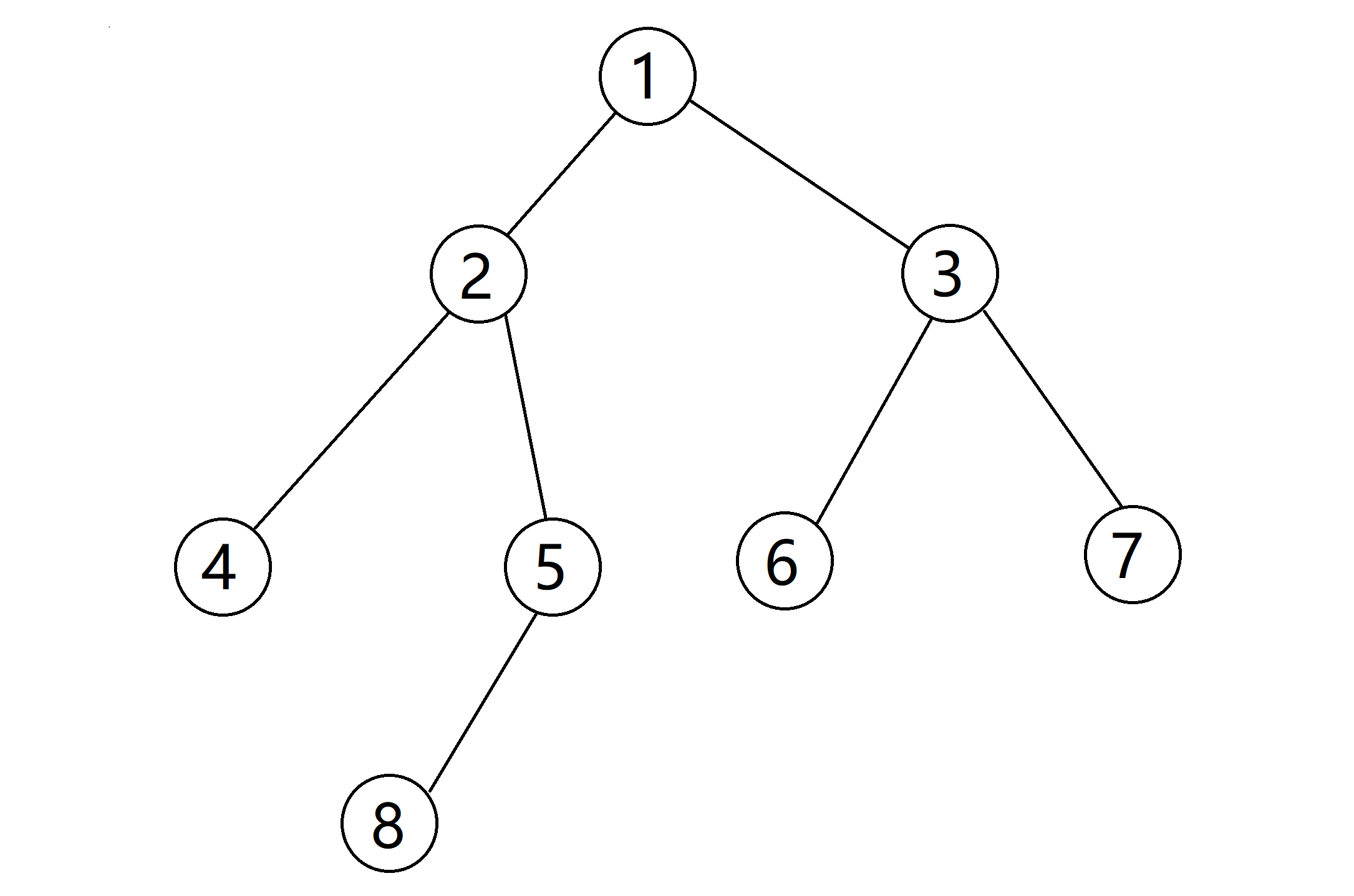
对于路径 $2 -> 1 -> 3 -> 6$ ，它是经过了根节点的，属于 $1$ 类路径。

对于路径 $4 -> 2 -> 5 -> 8$ ，它没有经过根节点 $1$，属于 $2$ 类路径。

对于第一类路径我们直接处理，对于第二类路径，递归处理当前根的儿子，在儿子里面处理，也就是说现在我们只需要处理第一类路径。

怎么确定这个根呢？显然根的好坏可以决定算法的复杂度。

因为每次是递归儿子，显然递归层数越少越好，什么情况下递归层数越少？当前根是当前树的重心时！

那么，整个算法的框架如下：

1
2
3
4
5
6
7
8
9
10
void solve(int u){//当前节点u
    当前树的当前根节点为u，统计第一类路径;
    做标记，当前点已经当过根了(总不可能一直是一个点当吧=。=)
    for(u的所有儿子){
        if(儿子当过根节点了)continue;
        去掉满足在一个子树条件的不合法答案;
        在儿子的子树中得到一个新的根节点;
        solve(新的根节点);
    }return;
}

其中，在儿子的子树中得到一个新的根节点如下：

现在在 $Solva(1)$ 函数中，并且现在循环到了 $1$ 的儿子 $3$ ，那么 $3$ 的子树就是灰色三角形中的三个节点，我们的新 $root$ 就是灰色三角形这棵树的重心，现在刚开始的时候可以将 $3$ 看成根节点，然后再往下计算。

0X1F—-2 获取树的重心

很简单，只需要一个 $DP$ 就行了。

1
2
3
4
5
6
7
8
9
10
11
12
void getroot(int u,int fa){
    size[u]=1;mxss[u]=0;
    for(int v,i=head[u];i;i=G[i].nxt){
        if((v=G[i].to)==fa||vis[v])continue;
        getroot(v,u);
        size[u]+=size[v];
        mxss[u]=max(mxss[u],size[v]);
    }
    mxss[u]=max(mxss[u],sum-size[u]);
    if(mxss[u]<mxss[root])root=u; 
    //mxss[u]为u的子树中size最大的size，size就是u下面的子树大小。
}

那么这一句是什么意思呢：mxss[u]=max(mxss[u],sum-size[u]);

我们再举个栗子，假如现在的 $u$ 是 $1$ ：($Qiuly$懒所以用的前面的那个图)

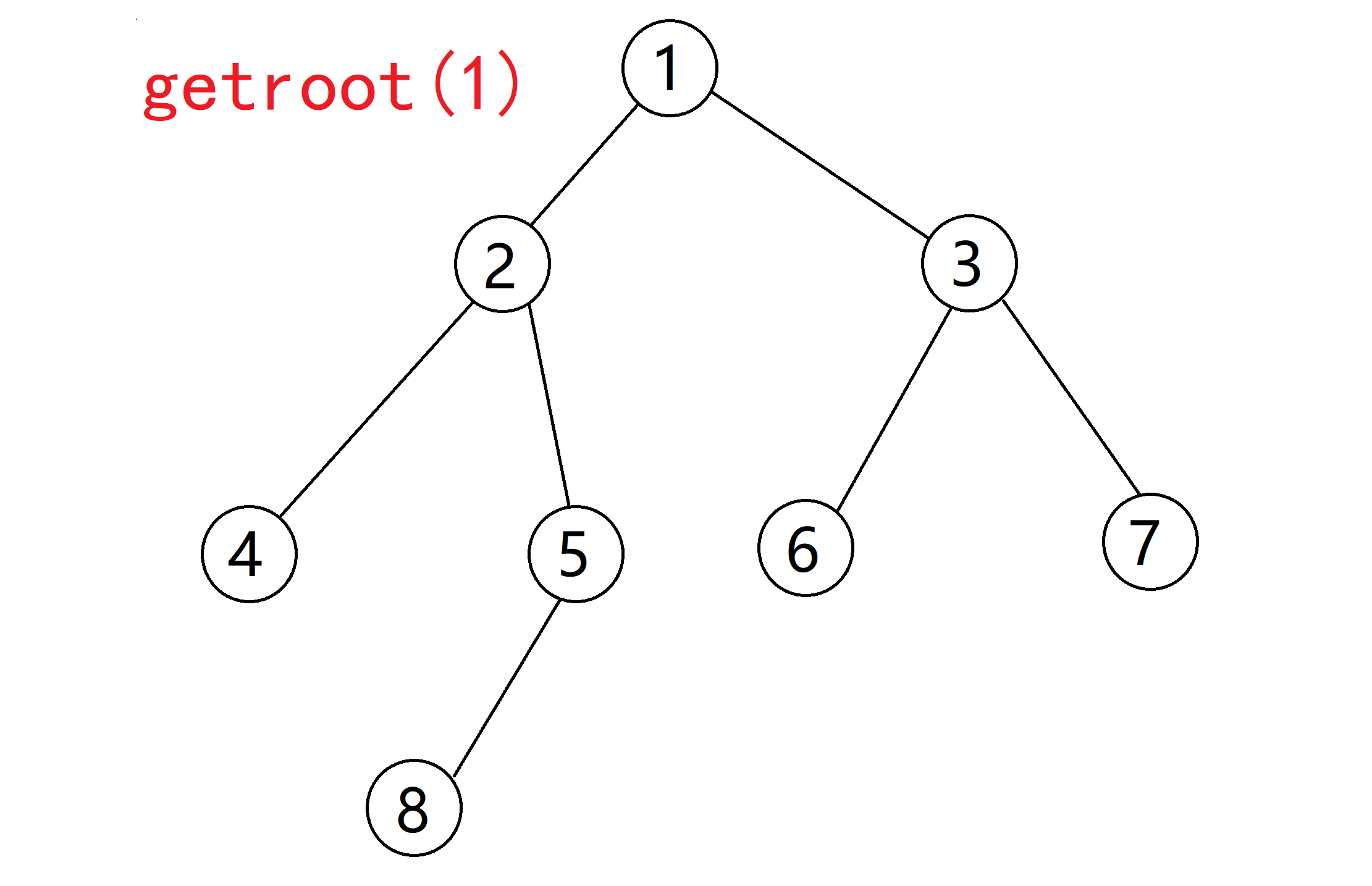
但是 $size[1]$ 统计的只是Ta下面的 ${2,3,4,5,6,7,8}$ 号节点，万一当前树不止这些呢？也就是说上面还有一坨节点，如果计算的时候显然也是要考虑进去的。

0X1F—-怎么统计1类路径？

Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void getdist(int u,int fa){
    use[++cnt]=dist[u];
    for(int v,i=head[u];i;i=G[i].nxt){
        if((v=G[i].to)==fa||vis[v])continue;
        dist[v]=dist[u]+G[i].val;getdist(v,u);
    }return;
}

int calc(int u,int dist0){
    cnt=0;dist[u]=dist0;
    getdist(u,0);
    std::sort(use+1,use+1+cnt);
    int l=1,r=cnt,res=0;
    while(l<r)
       if(use[l]+use[r]<=k)res+=r-l,++l;
       else --r;
    return res; 
}

确定了当前树的 $root$ 后，我们可以定义 $dist[root]$ 为 $0$ ，其余的当前树的节点的 $dist$ 为Ta到 $root$ 的距离(路上所有边的权值和)。

显然，这个问题很容易搞定($getdist$)。

想象一下，现在有一条路径 $l -> \cdots -> root -> \cdots -> r$，显然这条路径的权值就是 $dist[l] + dist[r]$。

可是，如果一一去枚举 $l,r$ 并且统计的话复杂度是报表的啊！
这没关系，我们依旧可以用线性的时间复杂度解决问题。

得到了所有的 $dist$ 后，我们排个序。

然后就是统计的流程。

假设现在排好序的数列为 {$1,1,2,3,4,4,5,6,7,7,8$}，$l$ 为 $1$ ，$r$ 为 $cnt$。

现在计算 $1+8$ ，显然如果 $1+8$ 小于 $k$ ，那么 $1 + (1/2/3/4/4/5/6/7/7)$ 都会小于 $k$，这个时候直接统计即可。否则 --r ，因为我们还需要统计的是 $l+1,l+2,\cdots$，既然这个 $r$ 不行了，对后面的答案是肯定不会有影响的。

最后 $return;$

0X2F 总体代码

Test:Luogu P4178 Tree

Code:如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
//为了格式不鬼畜这两个宏定义我只能放着了QvQ
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm> 

const int N=4e4+2;
const int inf=1e9+9;

int n,m,k,cnt,sum,ans,root,head[N];
int vis[N],use[N],dist[N],size[N],mxss[N];
struct Edge{
    int nxt,to,val; 
}G[N<<1];

template <typename _Tp> inline void IN(_Tp&x){
    char ch;bool flag=0;x=0;
    while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    if(flag)x=-x;
}

void getroot(int u,int fa){
    size[u]=1;mxss[u]=0;
    for(int v,i=head[u];i;i=G[i].nxt){
        if((v=G[i].to)==fa||vis[v])continue;
        getroot(v,u);
        size[u]+=size[v];
        mxss[u]=max(mxss[u],size[v]);
    }
    mxss[u]=max(mxss[u],sum-size[u]);
    if(mxss[u]<mxss[root])root=u; 
}

void getdist(int u,int fa){
    use[++cnt]=dist[u];
    for(int v,i=head[u];i;i=G[i].nxt){
        if((v=G[i].to)==fa||vis[v])continue;
        dist[v]=dist[u]+G[i].val;getdist(v,u);
    }return;
}

int calc(int u,int dist0){
    cnt=0;dist[u]=dist0;
    getdist(u,0);
    std::sort(use+1,use+1+cnt);
    int l=1,r=cnt,res=0;
    while(l<r)
       if(use[l]+use[r]<=k)res+=r-l,++l;
       else --r;
    return res; 
}

void solve(int u){
    ans+=calc(u,0);
    vis[u]=1;
    for(int v,i=head[u];i;i=G[i].nxt){
        if(vis[(v=G[i].to)])continue;
        ans-=calc(v,G[i].val);
        sum=size[v];root=0;
        getroot(v,0);
        solve(root);
    }return;
}

int main(){
    IN(n),sum=mxss[0]=n;
    for(int i=1,u,v,w;i<n;++i){
        IN(u),IN(v),IN(w);
        G[++cnt]=(Edge){head[u],v,w};head[u]=cnt;
        G[++cnt]=(Edge){head[v],u,w};head[v]=cnt;
    }
    IN(k);
    getroot(1,0);
    solve(root);
    printf("%d\n",ans);
    return 0; 
}

Test:Luogu P3806 【模板】点分治1

Analysis:

很显然我们不能像上面那样傻乎乎的While了，那样不能算出路径的权值，只能统计。
干脆统计时来个双重循环暴力吧！然后搞个桶。复杂度很高但是能过得了(至少这一题是这样的)

Code:如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
//Q.v.Q........................
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#define ll long long
#define RI register int 

const int N=1e4+2;
const int inf=1e9+9;

int ans[10000005];
int n,m,k,cnt,sum,root,head[N];
int vis[N],use[N],dist[N],size[N],mxss[N];
struct Edge{
    int nxt,to,val; 
}G[N<<1];

template <typename _Tp> inline void IN(_Tp&x){
    char ch;bool flag=0;x=0;
    while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    if(flag)x=-x;
}

void getroot(int u,int fa){
    size[u]=1;mxss[u]=0;
    for(int v,i=head[u];i;i=G[i].nxt){
        if((v=G[i].to)==fa||vis[v])continue;
        getroot(v,u);
        size[u]+=size[v];
        mxss[u]=max(mxss[u],size[v]);
    }
    mxss[u]=max(mxss[u],sum-size[u]);
    if(mxss[u]<mxss[root])root=u; 
}

void getdist(int u,int fa){
    use[++cnt]=dist[u];
    for(int v,i=head[u];i;i=G[i].nxt){
        if((v=G[i].to)==fa||vis[v])continue;
        dist[v]=dist[u]+G[i].val;getdist(v,u);
    }return;
}

void calc(int u,int dist0,int add){
    cnt=0;dist[u]=dist0;
    getdist(u,0);
    for(int i=1;i<=cnt;++i)
       for(int j=1;j<=cnt;++j)
          ans[use[i]+use[j]]+=add; 
}

void solve(int u){
    calc(u,0,1);vis[u]=1;
    for(int v,i=head[u];i;i=G[i].nxt){
        if(vis[(v=G[i].to)])continue;
        calc(v,G[i].val,-1);
        sum=size[v];root=0;
        getroot(v,0);
        solve(root);
    }return;
}

int main(){
    IN(n),IN(m),sum=mxss[0]=n;
    for(int i=1,u,v,w;i<n;++i){
        IN(u),IN(v),IN(w);
        G[++cnt]=(Edge){head[u],v,w};head[u]=cnt;
        G[++cnt]=(Edge){head[v],u,w};head[v]=cnt;
    }
    getroot(1,0);
    solve(root);
    for(int i=1;i<=m;++i)
       IN(k),printf(ans[k]?"AYE\n":"NAY\n");
    return 0; 
}

~~(还是背板子最重要嘿嘿嘿)

本文标题:【算法】 点分治总结&学习笔记

文章作者:Qiuly

发布时间:2019年02月13日 - 00:00

最后更新:2019年03月29日 - 13:51

原始链接:http://qiulyblog.github.io/2019/02/13/[算法]点分治/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。